There are some things I like about the culture of classical music, and some things I really, really don't. For instance, I love the idea that music is more than just an accompaniment to something else (like a movie), and more than mere entertainment. Though this obviously isn't exclusive to the type of music we call classical, I still see it as one of the prominent features of classical music, what motivates it and defines it, since the actual music can't really be fit into any one single category or united by any style or idea.
(Just like the music itself, it's hard to fit "the culture of classical music" into a single box, since it's different to different people. Nevertheless, I maintain that for better or worse, the common understanding of the words "classical music" in the world today is more or less a definition of a type of listening setting and a set of conventions, though these conventions aren't universally agreed on or anything like that.)
Anyway, what I don't like is that classical music tends to bring along an obsession with the past—preserving it, reproducing it, elevating it. Now, don't get me wrong, I love music from the past; how else would I have made it through 20+ years of education in Western music? There's a lot of great music out there, and I think it's well worth keeping around for the next hundred, thousand, million years.
But there's also a lot, lot, lot of music that was written in Europe between 1600-1900 (give or take), and listening to it comes with an opportunity cost of keeping up with something more current. If you try to listen to all of the music from this period, you're necessarily missing out on a lot of other music, and you're necessarily going to hear a lot, lot, lot of music that kinda sounds like Mozart, Bach, or Beethoven, except that it's not nearly as good. Like, say, this!
I didn't have to look very hard for this, by the way. All I did was go to WETA (my local classical radio station) and pick literally the first thing on the playlist for today. The rest of the list is littered with other music that, at its best, is mildly pleasant, and at its worst, is incredibly boring.
I have nothing against Carl Friedrich Abel. I'm sure he was a nice guy. I'm sure there's something interesting about him, to an academic somewhere in the world. But is this the music that people who have any sort of direction over the future of classical music should be promoting? What makes this music worth playing, worth listening to?
I understand that radio stations are playing to their audience, and that I never contribute to them. But I do believe there is some top down influence on people's preferences. (And I would contribute to the station if it weren't so terrible and made more creative selections.)
I imagine the executives of WETA claim they are carrying on a proud and longstanding tradition of a certain variety of Western music, but really they're just peddling mediocrity. What brings Abel to the airwaves is the convenient-but-not-at-all distinguishing fact that he happened to write music the kinda sounds like Mozart (if you're half-asleep) written around the same time and place as Mozart. Is that a reason to listen to a piece of music? I say no. Overall, they (institutions like WETA) make it difficult, as an omnipresent standard-bearer of classical music in the DC area to forge a future for concert music that is interesting, diverse, enjoyable, and dynamic.
(Full disclosure, they sponsor the music where I teach; obviously this post does not reflect the opinions of the school and would probably horrify them. Sorry, Levine!)
Sam's Posts
Thoughts on soccer, science, politics, and the arts
Tuesday, May 10, 2016
Sunday, April 24, 2016
Excellent sheep in music education
In 2014, a former Yale English professor published a provocative book following an essay in the American Scholar. His central idea: the elite institutions of American higher education, from high-priced secondary schools to prestigious universities, increasingly value, encourage, and churn out students who are very good at jumping through hoops on a path to achievement (so-called "excellent sheep") without engaging in real intellectual risk-taking and discovery. Though I felt somewhat differently about my own experience at an elite institution, there is one subject where I felt and continue to experience exactly what he's talking about: music education.
Music education, of course, comes in many different strains and variations, and within any system or institution there are always exceptions. But any student in a traditional classical performance program will recognize the excellent-sheep-ist attitude that propels us from conservatory preparatory programs through college and graduate school, funneling many of us (in some sense, the lucky ones) into orchestras and competitions after graduation. To put it bluntly, a traditional instrumental music education is largely and predominantly about execution as opposed to creation: how to execute precisely, exactly, and perfectly the music on the page in front of you.
Full disclosure: I am a piano teacher at a school that is very much part of the system I'm writing about, though it is better than most, and moving in the right direction. But I am part of the problem too. Another disclosure: obviously there are times and situations where execution is paramount (especially in large ensembles). But that doesn't mean it needs to be the singular focus of an education.
First, we teach children to read music and show them exactly what all the symbols mean in front of them. We teach them technique and exercises so that they have the freedom to play anything, but if that anything is written down in front of them, then we generally demand they play it a certain way.
I can hear some of my friends and colleagues crying out, "but there's so much room for creativity in different manners of execution!" And that is true, but even there the role of creativity, of personal artistic freedom, is often minimized in service to the original creator of the music.
Think I'm simplifying? Don't believe me? Let's look to some authorities of classical music. Sviatoslav Richter is widely considered one of the greatest pianists of the 20th century, and he described his thinking thusly: "The interpreter is really an executant," (emphasis mine), "carrying out the composer's intentions to the letter. He doesn't add anything that isn't already in the work." It wasn't hard to find this blog post from renowned cellist Lynn Harrell about his frustration with students' imposing—get this!—their own wills on musical performances. Other examples explicitly urging forth excellent sheep from the Internet abound.
The philosophical problem with these types of views, though dominant in the conservatory world, are several, but in practice they tend to fuse everyone's playing together, encouraging a sameness across the world of music. A performance in this view is less an act of creative expression than a fact-finding mission, a piece of detective work. Is that really what we want?
Ironically, Richter himself came up with some of the bizarre and enigmatic performances of the music of Brahms, Schubert, etc., and that's what truly made him a great pianist, at least for me. In fact, is there any artist, musician or otherwise, performer or otherwise, for whom anyone holds the highest admiration, merely for playing exactly by the rules and strictures handed down from above?
Thankfully, I've had some wonderful teachers in my own education, but I believe it's time for classical music to reckon with its authoritarian attitude and priorities. A music education should emphasize execution in the service of expression. It should include spontaneity, improvisation and creation, in addition to tradition. How to do that? Coming up next time...
Music education, of course, comes in many different strains and variations, and within any system or institution there are always exceptions. But any student in a traditional classical performance program will recognize the excellent-sheep-ist attitude that propels us from conservatory preparatory programs through college and graduate school, funneling many of us (in some sense, the lucky ones) into orchestras and competitions after graduation. To put it bluntly, a traditional instrumental music education is largely and predominantly about execution as opposed to creation: how to execute precisely, exactly, and perfectly the music on the page in front of you.
Full disclosure: I am a piano teacher at a school that is very much part of the system I'm writing about, though it is better than most, and moving in the right direction. But I am part of the problem too. Another disclosure: obviously there are times and situations where execution is paramount (especially in large ensembles). But that doesn't mean it needs to be the singular focus of an education.
First, we teach children to read music and show them exactly what all the symbols mean in front of them. We teach them technique and exercises so that they have the freedom to play anything, but if that anything is written down in front of them, then we generally demand they play it a certain way.
I can hear some of my friends and colleagues crying out, "but there's so much room for creativity in different manners of execution!" And that is true, but even there the role of creativity, of personal artistic freedom, is often minimized in service to the original creator of the music.
Think I'm simplifying? Don't believe me? Let's look to some authorities of classical music. Sviatoslav Richter is widely considered one of the greatest pianists of the 20th century, and he described his thinking thusly: "The interpreter is really an executant," (emphasis mine), "carrying out the composer's intentions to the letter. He doesn't add anything that isn't already in the work." It wasn't hard to find this blog post from renowned cellist Lynn Harrell about his frustration with students' imposing—get this!—their own wills on musical performances. Other examples explicitly urging forth excellent sheep from the Internet abound.
The philosophical problem with these types of views, though dominant in the conservatory world, are several, but in practice they tend to fuse everyone's playing together, encouraging a sameness across the world of music. A performance in this view is less an act of creative expression than a fact-finding mission, a piece of detective work. Is that really what we want?
Ironically, Richter himself came up with some of the bizarre and enigmatic performances of the music of Brahms, Schubert, etc., and that's what truly made him a great pianist, at least for me. In fact, is there any artist, musician or otherwise, performer or otherwise, for whom anyone holds the highest admiration, merely for playing exactly by the rules and strictures handed down from above?
Thankfully, I've had some wonderful teachers in my own education, but I believe it's time for classical music to reckon with its authoritarian attitude and priorities. A music education should emphasize execution in the service of expression. It should include spontaneity, improvisation and creation, in addition to tradition. How to do that? Coming up next time...
Saturday, April 16, 2016
Speed Reading, Chess, and Playing by Ear
Recently I've taken to starting recitals by playing popular jingles from TV or radio shows. It's fun to see who else in the audience listens to Serial or NPR, or is familiar with the Champion's League theme (come on people, it may be the most widely-recognized music on the planet). Admittedly, it's also to win over the audience and impress them right off the bat, because rattling off something by ear is unusual and seldom taught in the world of (so-called) classical music and traditional music education (a topic for another time).
At the intermission of one show, someone asked me: can you play anything by ear, instantly? The answer is a definite and emphatic no, but the question reveals a lot about people's misunderstanding not just of music, but of human cognition and the limitations of memory.
People assume that playing music by ear is difficult because amateur listeners (and even amateur musicians, see: educational issues above) are not used to identifying pitches or the distances between them. Sadly for us musicians, identifying notes is only the first and easiest hurdle to clear when trying to learn music by ear. Remembering and rattling off a piece, armed only with the ability to identify pitches, would be like memorizing a poem by remembering the sequence of letters. The real problem is not identification but information reduction, taking a whole slew of sound and unconsciously reducing it to larger abstract musical components.
Think about the process you would go through in memorizing some lines of text to write out later. First, let's keep it simple, and imagine you just had to learn a single sentence, like, "What is your favorite piece of music and why do you like it?" Piece of cake, right?
But what if the line were in a foreign language that you didn't know ("Cila është pjesa juaj e muzikës dhe pse nuk ju pëlqen?" **from google translate, possibly not accurate)? In that case, your best bet would be remembering the sequence of letters that make up the spelling of the phrase. Think how difficult that might be for even a few words, how much more work, and how prone you would be to mistakes. Even worse, if you misremembered even just a couple of letters, it might distort the meaning or render the phrase completely meaningless. You couldn't remember it accurately with a single glance, even though remembering any of the individual component letters or words on their own might not be difficult at all. (In a language with different symbols, things would be an order of magnitude more difficult, though in principle the same: remembering any single letter in Arabic might not be too difficult, but good luck with a string of them).
The difference is, in your native language you don't have to remember the individual letters—or even words—that make up the phrase, but only a single concept (or two) of favorite-music-ness. If you mis-remembered the exact wording, you would still easily reproduce something that preserved the meaning ("What's your favorite piece of music and why do you love it so much?").
I was reading this morning (pretty quickly, but not that quickly) about speed-reading in the New York Times, and the problem is the same (though one level of abstraction higher). I used to think if my eyes could just move faster through text, I could read faster. But the limiting factor in reading isn't the speed of cramming letters and words into your brain through your eyes, it's remembering, keeping track of, and making sense of what your eyes are sending to your brain. Turns out, most people can only keep track of 5-9 "concepts" at a time, and so reading is really an exercise in grouping words into concepts, absorbing them, and then moving on. People who can "chunk" the most words into a single abstract idea or concept, then, will tend to be faster readers.
The go-to example in psychology textbooks is memory for chess positions. People used to think master chess players had great memories because they could remember an entire chessboard much more accurately than amateur players, but it turns out expert players are no better (or only slightly better) at remembering a randomly arranged board than amateurs. They're better with boards from real games because rather than store the pieces and their positions one by one, they store the board in relation to other "types" of positions they've seen before, and so only have to remember a few ideas, rather than all 32 pieces' positions.
I know very little about chess, so I can't really explain what those "types" are, but what I do know a lot about is music! And the process for learning something by ear is very similar, only the "types" of things you have to remember are music-specific instead of chess-specific. Identifying this pitch or that pitch from something you hear is essential, but it's only as helpful as remembering that the word "what's" starts with a w, or that white bishop is in position a6. In other words, it's a total red herring and completely misses the point. What's helpful in reproducing a musical phrase is reducing it to something close to something you've heard before and stored in memory already from hearing and categorizing thousands of times already, to a series of harmonies and rhythms and patterns that you already know.
One final story to clear up a musical misconception about absolute, or perfect, pitch. Absolute pitch is the ability to identify the pitch class of a sounded note (a, b, c, etc., basically, where it is on the piano). People sometimes think of absolute pitch as a great musical gift, and it doesn't hinder anything, but it's also, again, a red herring in terms of musical cognition. Example: a classmate who had absolute pitch in one of my music classes in high school. We were learning to identify different chord types (major, minor, etc.) by sound and by sight (hearing them or seeing them written down on the staff). Just as a point of reference, most of my beginner piano students can learn to do the sound identification task without too much difficulty. But rather than listen to the quality of the chord overall in the sound training, my fellow student would try to hear all the pitches individually, write them down, and then determine what type of chord was played by sight. In other words, instead of reducing the information, she was multiplying it! Like a great speller declaring, "I'll remember the phrase 'what's your favorite piece of music and why' by spelling it out each time, rather than storing its meaning." Moral: absolute pitch plays little to no role in musical memory since it generally doesn't help reduce information at all.
And even relative pitch (the ability to identify relationships between two pitches), while important and more valuable than perfect pitch, is only the first small step in learning to play by ear, since it, too, only aids the identification of pitches, but not necessarily the ability to store and remember those relationships.
At the intermission of one show, someone asked me: can you play anything by ear, instantly? The answer is a definite and emphatic no, but the question reveals a lot about people's misunderstanding not just of music, but of human cognition and the limitations of memory.
People assume that playing music by ear is difficult because amateur listeners (and even amateur musicians, see: educational issues above) are not used to identifying pitches or the distances between them. Sadly for us musicians, identifying notes is only the first and easiest hurdle to clear when trying to learn music by ear. Remembering and rattling off a piece, armed only with the ability to identify pitches, would be like memorizing a poem by remembering the sequence of letters. The real problem is not identification but information reduction, taking a whole slew of sound and unconsciously reducing it to larger abstract musical components.
Think about the process you would go through in memorizing some lines of text to write out later. First, let's keep it simple, and imagine you just had to learn a single sentence, like, "What is your favorite piece of music and why do you like it?" Piece of cake, right?
But what if the line were in a foreign language that you didn't know ("Cila është pjesa juaj e muzikës dhe pse nuk ju pëlqen?" **from google translate, possibly not accurate)? In that case, your best bet would be remembering the sequence of letters that make up the spelling of the phrase. Think how difficult that might be for even a few words, how much more work, and how prone you would be to mistakes. Even worse, if you misremembered even just a couple of letters, it might distort the meaning or render the phrase completely meaningless. You couldn't remember it accurately with a single glance, even though remembering any of the individual component letters or words on their own might not be difficult at all. (In a language with different symbols, things would be an order of magnitude more difficult, though in principle the same: remembering any single letter in Arabic might not be too difficult, but good luck with a string of them).
The difference is, in your native language you don't have to remember the individual letters—or even words—that make up the phrase, but only a single concept (or two) of favorite-music-ness. If you mis-remembered the exact wording, you would still easily reproduce something that preserved the meaning ("What's your favorite piece of music and why do you love it so much?").
I was reading this morning (pretty quickly, but not that quickly) about speed-reading in the New York Times, and the problem is the same (though one level of abstraction higher). I used to think if my eyes could just move faster through text, I could read faster. But the limiting factor in reading isn't the speed of cramming letters and words into your brain through your eyes, it's remembering, keeping track of, and making sense of what your eyes are sending to your brain. Turns out, most people can only keep track of 5-9 "concepts" at a time, and so reading is really an exercise in grouping words into concepts, absorbing them, and then moving on. People who can "chunk" the most words into a single abstract idea or concept, then, will tend to be faster readers.
The go-to example in psychology textbooks is memory for chess positions. People used to think master chess players had great memories because they could remember an entire chessboard much more accurately than amateur players, but it turns out expert players are no better (or only slightly better) at remembering a randomly arranged board than amateurs. They're better with boards from real games because rather than store the pieces and their positions one by one, they store the board in relation to other "types" of positions they've seen before, and so only have to remember a few ideas, rather than all 32 pieces' positions.
I know very little about chess, so I can't really explain what those "types" are, but what I do know a lot about is music! And the process for learning something by ear is very similar, only the "types" of things you have to remember are music-specific instead of chess-specific. Identifying this pitch or that pitch from something you hear is essential, but it's only as helpful as remembering that the word "what's" starts with a w, or that white bishop is in position a6. In other words, it's a total red herring and completely misses the point. What's helpful in reproducing a musical phrase is reducing it to something close to something you've heard before and stored in memory already from hearing and categorizing thousands of times already, to a series of harmonies and rhythms and patterns that you already know.
One final story to clear up a musical misconception about absolute, or perfect, pitch. Absolute pitch is the ability to identify the pitch class of a sounded note (a, b, c, etc., basically, where it is on the piano). People sometimes think of absolute pitch as a great musical gift, and it doesn't hinder anything, but it's also, again, a red herring in terms of musical cognition. Example: a classmate who had absolute pitch in one of my music classes in high school. We were learning to identify different chord types (major, minor, etc.) by sound and by sight (hearing them or seeing them written down on the staff). Just as a point of reference, most of my beginner piano students can learn to do the sound identification task without too much difficulty. But rather than listen to the quality of the chord overall in the sound training, my fellow student would try to hear all the pitches individually, write them down, and then determine what type of chord was played by sight. In other words, instead of reducing the information, she was multiplying it! Like a great speller declaring, "I'll remember the phrase 'what's your favorite piece of music and why' by spelling it out each time, rather than storing its meaning." Moral: absolute pitch plays little to no role in musical memory since it generally doesn't help reduce information at all.
And even relative pitch (the ability to identify relationships between two pitches), while important and more valuable than perfect pitch, is only the first small step in learning to play by ear, since it, too, only aids the identification of pitches, but not necessarily the ability to store and remember those relationships.
Monday, August 24, 2015
Trump Appealing to Broad and Diverse Coalition of Assholes, Survey Shows

Although many have "drawn comfort from the belief that Donald J. Trump’s dominance in the polls is a political summer fling", a new analysis shows that he is building a broad and diverse coalition of douchebags, jerks and straight up assholes to maintain his position at the top of the Republican primary field.
Trump draws enthusiasm from people of varying ideological, political and demographic backgrounds, but the data suggest his supporters do in fact fall squarely into one category: total dicks.
Republican Party strategists are particularly impressed at Trump's ability to unite this emerging and powerful voting bloc. "Sure, we're been courting the asshole vote for years," said one Republican insider. "But with his wishy-washy attitude toward attacking defenseless homeless people, Trump is setting a new bar."
Carl Tomanelli of Londonderry, N.H. counts himself among Trump's supporters. "People are starting to see, I believe, that all this political correctness is garbage," he said. "I think he’s echoing what a lot of people feel and say." Added Tomanelli, "And by people, I mean, you know, sexist and xenophobic jackasses."
Lisa Carey said, "As inappropriate as some of his comments are, I think it’s stuff that a lot of people are thinking but afraid to say. And I’m a woman." Continued Carey, "And, as you can clearly tell, I've thought through the consequences and wisdom of having the man responsible for the safety and well-being of over 300 million citizens casually blurt out the inappropriate things that other people are thinking."
In general, Trump's women supporters cited his willingness to be a total douche toward Mexicans as paramount to any policy concerns, while his sexist male enthusiasts pointed to an egregiously demeaning attitude toward women as key to their unconditional support.
Thursday, August 13, 2015
Study: literally looking at a single pie chart increases support for action on climate change

Ah, climate change policy. Forever frozen in a political standoff, impossible to move toward a consensus. Or is it?
Today I came across this study on PLOS via a link from the Times. As with most scientific papers, the core message is obscured by technical details and jargon (Gateway Belief Model??), but the takeaway is simple and powerful: inform people of the overwhelming scientific consensus that human-caused climate change is real, and their belief in that consensus, along with support for public action, increases. Democrats and Republicans alike. Voila!
The method of the experiment, likewise, was really basic. Step 1: ask people what their estimation of the state of the scientific consensus is around climate change (only 12% accurately put the consensus above 90% on initial questioning) along with a few other simple questions—whether they're worried about it, whether they support public action, etc. Step 2: inform them of the actual scientific consensus (via one-sentence script, pie chart, or convoluted metaphor). Step 3: repeat step 1.
I'm surprised this paper hasn't received more press, precisely because most of what you read about political opinions (not that this issue is actually political, of course!) suggests that you can't change people's mind on charged topics: people filter new information to confirm what they already believe and even harden their views in the face of conflicting evidence. I feel like I'm constantly barraged by articles in the media about the impossibility of shifting anyone's attitudes on any important, consequential topic by supplying information.
Take this recent example of an experiment about people's attitudes toward gay marriage. The study got a ton of attention because everyone was so shocked that talking to people (appeared to) succeed in shifting their attitudes on gay marriage. This American Life did a whole show about it! The study's conclusions were also really narrow: only protracted, personal and empathetic conversations were effective in changing people's views (as opposed to reading a prepared script or set of facts). Furthermore, it turned out the entire dataset was fabricated, so it's possible no one's views changed at all.
That's why this climate change study is really encouraging, and kind of shocking. Caveats: it's just one experiment and the results, while robust, are modest (4 point mean increase in people's belief, on a scale of 1-100, that humans are causing the climate to change, and 1.7 point mean increase in people's belief that people should be doing more to reduce climate change). Still, that's pretty good for one sentence, pie chart, or metaphor.
What's going on? Are people more open to new facts and shifting their views than previous research suggests, or is climate change different from other political issues associated with complete and utter intransigence like abortion, evolution in education, gun control, etc?
I'm guessing it's a little of both, but mostly the latter. Unlike abortion, evolution, or gay marriage, climate change denial isn't a result of core philosophical or theological beliefs, even loosely defined. It's not even a longstanding political divide (the first President to propose cap and trade climate legislation was George W Bush). Which suggests that elite political opposition to climate change policy, far from an inevitable result of climate change denial, may actually be a principal cause. That, at least, is the simplest explanation for people's ignorance of the scientific consensus in the first place.
So, ya know, in case you were wondering:

Friday, December 19, 2014
Serial's fallacies and how we fell for them
At the beginning of Serial, Sarah Koenig and Ira Glass convinced me I was in for a wild ride. I was supposed to live Koenig's back-forth-experience of doubt and conviction. Adnan is innocent—no, he's guilty! Every episode, a new telling clue, a new revelation!
Little did I know Koenig and her producers had no idea how to incorporate new evidence with their prior beliefs. They fell prey—repeatedly—to the prosecutor's fallacy, giving undue weight to new discoveries, trying to pull us along as they changed sides again and again. Unfortunately for them, the basic story never changed. At the beginning, there was no physical evidence against Adnan, and the whole case against him came down to Jay's credibility. In the end, there's no physical evidence against Adnan, and the whole case against him comes down to Jay's credibility.
Whenever Koenig was convinced of his innocence, something new—the Nisha call!—would change her mind. When she was almost convinced of his guilt, something different—the Aisha call!—would change it back. In the last episode, my frustration reached its peak when Dana—the "logical" one—summed up her understanding of the case with one telling instance of the prosecutor's fallacy. She argued that, despite the utter lack of evidence incriminating him, Adnan most likely killed Hae because the string of events that took place on the day of Hae's disappearance just make more sense that way, and are so unlikely if Adnan is innocent. I mean, if there's only a 10% chance that all of those unlucky coincidences would happen in the case of Adnan's innocence (the Nisha call, lending Jay his car and phone, asking Hae for a ride), then that means there's a 90% chance he did it, right??
Wrong. Turn that same argument on someone who wins the lottery. It's immensely unlikely, after all, for someone to win the lottery. But maybe she cheated. She's much more likely to win by cheating! There's only a 1/1000,000 chance of winning in the case of not cheating, so clearly, cheating is the more "logical" explanation.
The problem is with treating new pieces of evidence—winning the lottery, potentially unlucky coincidences—in isolation, rather than weighting them by prior likelihood. Yes, one is more likely to win the lottery by cheating, and yes, the Nisha call makes more sense if Adnan is guilty, but the prior probabilities in this case—of cheating at the lottery, of Adnan committing murder—are low. And that's what Koenig was missing throughout Serial, at every turn, in weighing evidence for or against Adnan.
And of course, there's a foolproof way to incorporate new beliefs with old ones: Bayes' rule, the most misunderstood of mathematical truths.
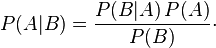
Or
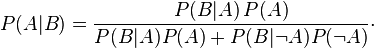
For instance, consider Dana's mental calculation at the end. She's looking at these coincidences more or less in isolation, as if they make up most of the case against Adnan (which, aside from Jay's questionable testimony, they kinda do). That is, she's considering the probability of Adnan's guilt (A) given the coincidences (B). Dana incorrectly equates this probability with P(B|—A), probability of B given not A, or the probability of those coincidences, given that Adnan is not guilty, which is of course low. Let's say 10% for the sake or argument. But as you can see, the two things are just not equivalent (this is the prosecutor's fallacy, more or less).
Let's estimate the other quantities reasonably. Let's imagine P(B|A), the probability of all of these unlucky things happening in the case Adnan is guilty, is high, say, 70%. (I wouldn't say 100%, even for the sake of argument, because why would Adnan call Nisha in the course of a murder?? All these things happening together is unlikely, even if Adnan is guilty).
Then there's P(A), the prior estimation of probability that Adnan murdered Hae, before we consider the evidence at hand. This has to be low, because Dana is using these coincidences to weigh Adnan's story against Jay's. And aside from that story, what reason do we have to believe Adnan committed the murder? Not much. So let's say this is 20% (still an overestimation, as well, I would say).
This leaves P(—A) = 1 - 20% = 80%, and our calculation is: (.7)*(.2) / [(.7)*(.2) + (.1)*(.8)] = .64
After weighing the evidence of these coincidences, our subjective probability that Adnan is guilty goes up, as we would expect. But not as high as we would think. Definitely not to 90%, as Dana kinda-sorta-implies but without any numbers. And I would argue that the 10% for P(B|—A) we chose was too low anyway, since we know Adnan had other potential reasons for lending his phone and car to Jay, and we know there are other possibilities for how the Nisha call could have happened. (And I don't know why they kept considering the cell tower evidence, since my understanding is that the tower just isn't that closely related to the location of the call).
This same process seemed to take place over and over again in Serial. Something new would come up, and Sarah Koenig would overstate its significance. Adnan stole money from the mosque: maybe he has the personality to commit murder. Aisha called Adnan when he was high at Jen's house: Adnan had a reason to be acting scared of the police. These may have made for compelling drama early on, but ultimately, turned Serial into a frustrating experience, because after the first few episodes, nothing of any substance happened or changed. The case against Adnan was comically thin all along, and the producers of Serial failed to break the story down much further than that.
In the end, it all came down to your P(A), your estimation of the prior likelihood of Adnan committing the murder after considering the basic evidence, and so everyone's opinion pretty much lined up with whom they believe more, Adnan or Jay. And in that sense, the whole series was a massive exercise in confirmation bias.
Little did I know Koenig and her producers had no idea how to incorporate new evidence with their prior beliefs. They fell prey—repeatedly—to the prosecutor's fallacy, giving undue weight to new discoveries, trying to pull us along as they changed sides again and again. Unfortunately for them, the basic story never changed. At the beginning, there was no physical evidence against Adnan, and the whole case against him came down to Jay's credibility. In the end, there's no physical evidence against Adnan, and the whole case against him comes down to Jay's credibility.
Whenever Koenig was convinced of his innocence, something new—the Nisha call!—would change her mind. When she was almost convinced of his guilt, something different—the Aisha call!—would change it back. In the last episode, my frustration reached its peak when Dana—the "logical" one—summed up her understanding of the case with one telling instance of the prosecutor's fallacy. She argued that, despite the utter lack of evidence incriminating him, Adnan most likely killed Hae because the string of events that took place on the day of Hae's disappearance just make more sense that way, and are so unlikely if Adnan is innocent. I mean, if there's only a 10% chance that all of those unlucky coincidences would happen in the case of Adnan's innocence (the Nisha call, lending Jay his car and phone, asking Hae for a ride), then that means there's a 90% chance he did it, right??
Wrong. Turn that same argument on someone who wins the lottery. It's immensely unlikely, after all, for someone to win the lottery. But maybe she cheated. She's much more likely to win by cheating! There's only a 1/1000,000 chance of winning in the case of not cheating, so clearly, cheating is the more "logical" explanation.
The problem is with treating new pieces of evidence—winning the lottery, potentially unlucky coincidences—in isolation, rather than weighting them by prior likelihood. Yes, one is more likely to win the lottery by cheating, and yes, the Nisha call makes more sense if Adnan is guilty, but the prior probabilities in this case—of cheating at the lottery, of Adnan committing murder—are low. And that's what Koenig was missing throughout Serial, at every turn, in weighing evidence for or against Adnan.
And of course, there's a foolproof way to incorporate new beliefs with old ones: Bayes' rule, the most misunderstood of mathematical truths.
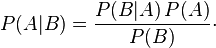
Or
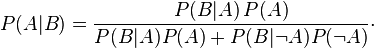
For instance, consider Dana's mental calculation at the end. She's looking at these coincidences more or less in isolation, as if they make up most of the case against Adnan (which, aside from Jay's questionable testimony, they kinda do). That is, she's considering the probability of Adnan's guilt (A) given the coincidences (B). Dana incorrectly equates this probability with P(B|—A), probability of B given not A, or the probability of those coincidences, given that Adnan is not guilty, which is of course low. Let's say 10% for the sake or argument. But as you can see, the two things are just not equivalent (this is the prosecutor's fallacy, more or less).
Let's estimate the other quantities reasonably. Let's imagine P(B|A), the probability of all of these unlucky things happening in the case Adnan is guilty, is high, say, 70%. (I wouldn't say 100%, even for the sake of argument, because why would Adnan call Nisha in the course of a murder?? All these things happening together is unlikely, even if Adnan is guilty).
Then there's P(A), the prior estimation of probability that Adnan murdered Hae, before we consider the evidence at hand. This has to be low, because Dana is using these coincidences to weigh Adnan's story against Jay's. And aside from that story, what reason do we have to believe Adnan committed the murder? Not much. So let's say this is 20% (still an overestimation, as well, I would say).
This leaves P(—A) = 1 - 20% = 80%, and our calculation is: (.7)*(.2) / [(.7)*(.2) + (.1)*(.8)] = .64
After weighing the evidence of these coincidences, our subjective probability that Adnan is guilty goes up, as we would expect. But not as high as we would think. Definitely not to 90%, as Dana kinda-sorta-implies but without any numbers. And I would argue that the 10% for P(B|—A) we chose was too low anyway, since we know Adnan had other potential reasons for lending his phone and car to Jay, and we know there are other possibilities for how the Nisha call could have happened. (And I don't know why they kept considering the cell tower evidence, since my understanding is that the tower just isn't that closely related to the location of the call).
This same process seemed to take place over and over again in Serial. Something new would come up, and Sarah Koenig would overstate its significance. Adnan stole money from the mosque: maybe he has the personality to commit murder. Aisha called Adnan when he was high at Jen's house: Adnan had a reason to be acting scared of the police. These may have made for compelling drama early on, but ultimately, turned Serial into a frustrating experience, because after the first few episodes, nothing of any substance happened or changed. The case against Adnan was comically thin all along, and the producers of Serial failed to break the story down much further than that.
In the end, it all came down to your P(A), your estimation of the prior likelihood of Adnan committing the murder after considering the basic evidence, and so everyone's opinion pretty much lined up with whom they believe more, Adnan or Jay. And in that sense, the whole series was a massive exercise in confirmation bias.
Tuesday, December 9, 2014
Dick Cheney to Senate: Nobody Out-Evils Dick Cheney
In scathing comments regarding the recently released Senate Intelligence report on the CIA's torture of detainees, Dick Cheney lambasted the committee for ignoring his "singular role" in creating "the policies, culture and dubious legal cover" for the CIA's interrogation techniques.
While the report contends that CIA interrogators acted without authorization and outside the legal bounds of the programs approved by the Bush administration, Cheney insists that he was behind the torture of the terrorist suspects all along. "This idea that detainees were waterboarded, deprived of sleep or subjected to 'rectal hydration' without my knowledge is absurd, since everyone knows I practically invented rectal hydration," said Cheney.
Insisting that he would have "personally waterboarded every detainee in US custody, guilty or innocent," Mr. Cheney dismissed the claim that the CIA acted as a rogue agent in the aftermath of the September 11th attacks.
"Look, I think it's become pretty clear the most outrageously terrible ideas from the last Presidential administration were my idea. Nobody at the CIA could have come up with anything this ill-conceived and ineffective," said the former Vice President, adding, "Nobody out-evils Dick Cheney."
Friday, November 7, 2014
Newly Discovered Fossil—and Science—Could Prove Problem for Creationists

As the Washington Post reports, researchers have discovered a fossil that they claim—along with the entirety of the scientific literature of the past 150 years—could be a headache for Biblical Creationists.
The new fossil may, along with multiple lines of converging evidence from fields as diverse as paleontology, biology, astronomy, genetics, physics and geology, finally provide strong evidence against the hypothesis that the world was created in its present form as little as 10,000 years ago.
"Sure, we have plenty of evidence from carbon dating that the earth is billions of years old," said lead researcher, Ryosuke Motani. "The theory of continental drift makes it pretty clear that the earth has changed quite a bit over that time. Once you get into the biology, you've got evidence from molecular genetics, comparative anatomy of homologous traits, not to mention the distribution of various branches of the tree of life around the globe, to name just a few."
Added Motani, "but until today, we didn't really have a smoking gun."
Multiple scientific observers have expressed hope that, along with many cases of observed evolution in nature and in laboratories, and in addition to numerous already-discovered fossils that appear to be the intermediate stages between marine and land-dwelling animals, the newly discovered fossil will be the straw that breaks the camel's back in the Creationists' argument.
"We truly believe that Creationist fundamentalists the world over will finally yield on this," an assistant researcher said. "...especially after they consider that nothing in the last century of scientific investigation has produced any shred support for their hypothesis."
A spokesman at the Creation Museum in Petersburg, Kentucky said they will take a "very close look" at the group's forthcoming research paper before deciding their next move.
Monday, October 20, 2014
Podcast! The Music Post is here
The Music Post is here! It's a podcast dedicated to discovering what makes great music great.
Listen to the first episode above, or right click here and select "save link as" to download directly.
You can also find episode two and all future episodes here, and subscribe on iTunes here.
Should be available for subscription on iTunes within a few days!
Okay, now why would I do such a thing?
In the past five years, I've played a lot of performances, and received a lot of feedback from audiences. A fair amount of this feedback comes in the form of praise for the feat of performing, things like "That looked so difficult" or "I can't believe you memorized that whole piece." Of course, I appreciate this type of praise, but as a musician, it's definitely not what I'm going for, because music, after all, isn't a sport. It's art.
What I'm really shooting for in a performance is to have the audience fall in love with whatever I'm playing, to seek it out. I know I've really, truly connected with an audience when people say something more like "That piece was so great! Where can I listen to it again?"
Even more effective than simply playing, I've found that walking people through a piece, pointing out features and motives, beautiful moments, is the surest way to get them to connect with it and seek it out later. Even more so than my playing, people appreciate these mini-explanations of the music I'm playing (or at least, that's what they claim!), telling me they've never been able to listen more closely or more attentively.
So I figure why restrict that to the recital hall? It scales perfectly well to a podcast, where you can listen while you drive, cook, or get ready for bed.
Hope you enjoy!
Listen to the first episode above, or right click here and select "save link as" to download directly.
You can also find episode two and all future episodes here, and subscribe on iTunes here.
Should be available for subscription on iTunes within a few days!
Okay, now why would I do such a thing?
In the past five years, I've played a lot of performances, and received a lot of feedback from audiences. A fair amount of this feedback comes in the form of praise for the feat of performing, things like "That looked so difficult" or "I can't believe you memorized that whole piece." Of course, I appreciate this type of praise, but as a musician, it's definitely not what I'm going for, because music, after all, isn't a sport. It's art.
What I'm really shooting for in a performance is to have the audience fall in love with whatever I'm playing, to seek it out. I know I've really, truly connected with an audience when people say something more like "That piece was so great! Where can I listen to it again?"
Even more effective than simply playing, I've found that walking people through a piece, pointing out features and motives, beautiful moments, is the surest way to get them to connect with it and seek it out later. Even more so than my playing, people appreciate these mini-explanations of the music I'm playing (or at least, that's what they claim!), telling me they've never been able to listen more closely or more attentively.
So I figure why restrict that to the recital hall? It scales perfectly well to a podcast, where you can listen while you drive, cook, or get ready for bed.
Hope you enjoy!
Monday, October 6, 2014
Art of Fugue, cont'd: which instruments?
Of the many mysteries surrounding the Art of Fugue, perhaps the most practical regards the instrumentation: Bach leaves no indication of what instrument(s) he had in mind in composing the piece. Perhaps it was just an oversight, or perhaps he thought it was so obvious, he didn't need to even write down the instruments. More likely, though, Bach was purposefully evasive and ambiguous, leaving the door open for numerous readings.
There's evidence to support multiple sides of the debate. The piece is written entirely in "open score," instead of on a grand staff as was most typical for keyboard music. On the other hand, various details suggest that Bach heard it on a keyboard (the fact that it's possible to play). For many people, Bach’s failure to explicitly commit to an
instrumentation—along with his failure/reluctance to indicate
tempos/dynamics/phrasings in the vast majority of his compositions—is a weakness or an unfortunate omission, opening this work, and all the works of Bach, to “wrong”
interpretations and gross manipulations.
But for me, it’s a strength, and maybe even a sign of Bach’s
foresight and growing wisdom in his old age. Why commit his final masterpiece
to any single instrument or ensemble when the world of music is always changing,
adapting to new trends? If a piece is to be timeless, it should adapt too, and
this is exactly what the Art of Fugue, and all of Bach’s music, has aged so
magnificently well. It’s the difference between “No state shall discriminate on
the basis of race” and “No state shall deny its citizens equal protection of
the laws.” The former may have been essentially what the drafters of the 14th
Amendment had in mind, but it would have been overly rigid, with no room for an
evolving standard of equality.
Questions of history and constitutional law aside, though, the practical question
remains: what instrumentation best suits this piece? Few works have been the
subject of more variety of interpretation. You can hear the Art of Fugue played
on piano, harpsichord, organ, harmonium, string quartet, brass
quartet, and recorder quartet, guitar and trombone duo (seriously), among others.
The advantage of the quartet versions is obvious: each
player can give his full attention to a single voice, giving them each an
independence that should—in theory at least—be impossible for a single keyboard
player to execute.
On top of that, compare moments like 0:38 in the video below to 0:34 in the video above. On the piano (though not the organ, to be discussed next time), you can't sustain notes. Once you play a note, it immediately starts to disappear. This is a huge disadvantage, in general, but even more so in the Art of Fugue, in places like this one. This moment brings back the main theme for the entire piece in a soaring soprano line, but on piano, it can be a little, well, disappointing.
On top of that, compare moments like 0:38 in the video below to 0:34 in the video above. On the piano (though not the organ, to be discussed next time), you can't sustain notes. Once you play a note, it immediately starts to disappear. This is a huge disadvantage, in general, but even more so in the Art of Fugue, in places like this one. This moment brings back the main theme for the entire piece in a soaring soprano line, but on piano, it can be a little, well, disappointing.
Then again, what we gain from hearing from four instruments' individuality and attention, we can easily lose in unity of vision and overall coherence. It's mighty difficult for one person to keep track of four voices, but at least that person is in full control and able to present one single vision of the music in question.
And then there’s the inescapable fact (for me, at least)
that this music just doesn’t quite sound right played on strings or brass
instruments. The main difference is in the quality of articulation on these
instruments vs the piano, harpsichord, or organ. On the latter instruments, it’s
impossible to play with a true legato,
or smoothness between the notes. Every note is marked by a clear and definite
beginning, unlike in string instruments (where the bow can continue moving
between notes), or winds and brass (air keeps flowing). This fact is something
we pianists work incredibly hard to overcome or compensate for, but it’s this
place in between, the illusion of legato that’s not quite there, that makes our
instrument perfect for contrapuntal writing. The quick-moving notes in the string parts have to be separated to be heard at all, but as such, they're too articulated, where on piano they can be with a more singing quality.
There are lots of other considerations, of course, and it depends on a lot on which number of the Art of Fugue we're talking about, as well as who exactly is playing. But perhaps not surprisingly, as a pianist, I think this music sounds best on a keyboard (and apologies to all brass player friends, but the brass quintet just doesn't work, at least not the one I linked above). But where I’m firmly convinced that much of Bach’s keyboard music sounds best on piano, specifically, I can’t say I’ve come to the same conclusion for the Art of Fugue. More on that next time.
For the record, this is my favorite non-keyboard version yet:
There are lots of other considerations, of course, and it depends on a lot on which number of the Art of Fugue we're talking about, as well as who exactly is playing. But perhaps not surprisingly, as a pianist, I think this music sounds best on a keyboard (and apologies to all brass player friends, but the brass quintet just doesn't work, at least not the one I linked above). But where I’m firmly convinced that much of Bach’s keyboard music sounds best on piano, specifically, I can’t say I’ve come to the same conclusion for the Art of Fugue. More on that next time.
For the record, this is my favorite non-keyboard version yet:
Thursday, September 25, 2014
The Hypnosis of Bach's Art of Fugue
A little over a year ago, I was driving along unsuspectingly when I switched on the car radio. Immediately I was taken, entranced by the incessant, interwoven lines of a four-part fugue played on the organ. I knew it could only be Bach, and moments later, when the original theme emerged in sustained and soaring whole notes in the soprano line, I knew it was from the Art of Fugue. Somehow, I had never heard any except the first, second, and fourth movements, or "Contrapunctuses," from one of Bach's last, culminating masterpieces. Sitting in city traffic is not usually the time or place we associate with profound experiences, but such was the power of Contrapunctus 9—and of Glenn Gould's playing—that I'll never forget those few minutes.
I went home and listened to more of the same recording, and was shocked at what I'd been missing. I know a lot of Bach's music, and have been lucky enough to perform a good chunk of it as well: the Well-Tempered Clavier, many of the dance suites, the Italian Concerto. When I played the Goldberg Variations, I kind of thought I had conquered the most difficult, the most complex, the pinnacle of them all. Little did I know the Art of Fugue is like the Goldberg Variations on steroids. In the words of Angela Hewitt, "it makes the Goldberg Variations sound like child's play."
These pieces are different from anything Bach wrote. They are beautiful, yes, and they can entertain, certainly. But at their best, they overwhelm, they awe, and they mesmerize.
The whole project consists of eleven fugues, plus four canons, plus six more "mirror" fugues, plus the final, colossal-yet-tragically-unfinished quadruple fugue, all labeled with the somewhat more generic Latin "Contrapunctus," for "counterpoint."
Why the obsession with fugues? Bach was the unquestionable master of counterpoint. No one has been (or will for all eternity be) able to combine music of multiple independent parts to better entice and challenge the human brain. That's why listening to Bach's music can sometimes be "difficult": there's usually no one thing going on (no "melody") that draws your ear to the exclusion of other parts of the music; there is, rather, a bunch of melodies all at once, constantly vying for your (and the poor keyboard player's) attention.
But the payoff is enormous. To the extent that our enjoyment of art comes from subtly recognizing patterns, contrapuntal music provides a whole layer or dimension on which to built those patterns. And fugues—pieces defined by one (usually) to a few recurring musical ideas, twisted and transformed to varying degrees of recognizability—provide the perfect medium for a true craftsman to demonstrate his mastery of counterpoint. And Bach was the greatest craftsman of all.
The first fugue is smooth, filled with a feeling of emptiness and desolation. It never departs from the key of d minor yet never stands still, continuously in flux, with no clear structural boundaries or moments of repose. It is in one sense the simplest piece of the whole set, yet it is mysteriously elusive. Whereas the other fugues will draw heavily on increasingly elaborate technical feats of fugal style—stretto, inversion, augmentation and diminution—as well as an elaborate chromaticism that was a hundred years ahead of its time, this fugue is propelled by nothing more than its simple subject, which serves as the inspiration for all that follows.
After that, the the music grows in technical and harmonic complexity, as well as sheer density, culminating—at least temporarily—in the obsessive, relentless and truly manic Contrapunctus 11.
The four canons and six mirror fugues are even more esoteric in style, but underscore Bach's incredible ability to mold his music to his thematic ideas. (The mirror fugues, by the way, are kind of exactly what they sound like: each has a right-side-up version, and an upside-down version, to be presented separately in their completion...pretty incredible!).
But none of them matches the dignity, solemnity and profundity of the final fugue (Glenn Gould's all-time favorite, by the way)....
Perhaps it is not the easiest piece to become acquainted with, and doesn't exactly make for easy listening. But be careful: the Art of Fugue is apt to consume you as it has done for me over these past couple of months. And the best is yet to come!
Tuesday, September 9, 2014
Alex Ross Missed the Point
Having just read Alex Ross's typically eloquent essay from last week's New Yorker (hoping my opinion is still relevant a week later), I can't help but wonder whether he's missed the point.
Ross talks about the joys of scanning his collection of CDs, of reading the old liner notes, of the personal connection he feels to each recording by virtue of its real, physical existence. He laments the economics of online streaming, where royalty payments are so pathetic, only the artists who have no need for them can hope to earn anything from them. (Aside: I was legitimately excited last month when my Spotify income surged to $1.95.) Certainly, he realizes that not everyone agrees: "If I were a music-obsessed teen-ager today, I would probably be revelling in this endless feast, and dismissing the complaints of curmudgeons."
But the problem of the cloud reaches deeper than Mr. Ross realizes. All nostalgia and ethics aside, listening to music from the cloud changes the perceptual experience of listening. Technology has shortened and divided our attention in many ways, and listening to music is no exception. And that's bad news for classical music in particular.
CDs, LPs, and cassette tapes: music in these forms is (or was) a commitment. You made a decision to buy a recording and spent your hard-earned money on it. Any time you wanted to listen, you had to decide that you would listen, what you would listen to, and physically go through the motions of starting some sort of listening device, while remaining in the same place for the duration of the recording. Listening was expensive, not just because it cost money, but in the cost of setting it up and parking yourself somewhere to hear it (or carrying around a massive portable player).
One of my very first recordings was a cassette of the Bach inventions. Cassettes were terrible, of course, but they were great because I couldn't skip ahead in the tracks: they forced me to listen all the way through.
At that point I probably only had three of four classical recordings to choose from (along with a handful of Madonna and Alanis Morisette tapes). Every time I bought or received a new CD, it was an event! I always listened religiously until I knew the new recording inside out.
Sometime in middle school, I jumped on board the technological bandwagon (at the time, this consisted of acquiring something called a "MiniDisc") that allowed me to splice different parts of different CD tracks together. I thought this was great! I could finally take my favorite moments of every piece of music and listen to them next to each other, basking in the continuous ecstasy of musical climax after climax. But of course, things didn't work out that way, because a musical moment's power comes with context. Much of the power of the end of Beethoven's 7th Symphony, or Mahler's 2nd, or any piece, comes from all the buildup before it, and trying to cheat my way to that kind of musical epiphany was shortsighted and naive.
In college, I swung back in the other direction. Having bought a record player and inheriting a bunch of my parents' old records, it was like elementary school all over again, and I could listen for long stretches of time. Maybe listening to LPs was a waste of time at a university (sorry parents!), but once I went through the tiresome routine of removing a record, cleaning it, and putting it on, I was certainly going to try my best to enjoy it and absorb everything it had to teach.
Listening today takes neither time nor money. MiniDiscs never rose to popularity, but what replaced them is more efficient and much easier to use (and much, much cheaper). On its face, this seems great! I doubt I ever would have bought six different recordings of the Marriage of Figaro, but I do have them all in my Spotify. But every time I want to listen to something new, the number of choices is mind-boggling. And humans don't always deal with choices intelligently. If I don't like something new right away, I don't usually follow through and listen to it again, the way I always would with a new CD, until I was absolutely sure I didn't like it.
Streaming makes it easy, too easy, to listen to music. We can listen any time, anywhere, for whatever tiny duration we choose, without taking our attention from whatever other task we might be engaged in. If you're listening to Ke$ha and Taylor Swift, that's probably okay. Pop music can survive a five minute attention span. But "classical" or "art" music requires sustained engagement and attention in order to be fully appreciated and understood.
Cloud listening has the potential for good, but it doesn't lend itself to true listening. Unfortunately, that's what classical music depends on. The only solution: fight back against our habits!
Friday, November 23, 2012
teaching backward, calculus, part 1
Some (admittedly limited) experience teaching math and physics in high school has led me to believe that the standard approach to teaching calculus is misguided. The way we typically teach math, the solutions all come first, and then we teach students why those solutions exist. But problems always precede solutions in real life. Why not in the classroom?
Calculus was developed as a solution to a very specific problem: the motion of objects through space. Though its applications range far beyond that problem, that original problem remains by far the best way to approach calculus since everybody already has intuition and experience with moving objects.
In a better world, then, calculus will always be approached from a physical perspective, since everyone already (sort of, at least) understands how things move around. Here's how. [This is, incidentally, what I did in the first day of AP physics class, but as you'll see, it's not terribly complicated, and (hopefully) most anyone can follow it.]
Imagine you're standing around with a stopwatch on a road that conveniently has length measurements posted all along it, and a car drives past you. Your task is to measure how fast the car is going the instant it passes the mark that's right at your feet. How do you do it?
Well, speed is just a measure of how far the car goes in some unit of time, say, a second, so you can just start your watch as the front wheels pass the mark by your feet, and then mark off where the front wheels of the car are when the watch reads exactly one second. (We can ignore the fact that, perceptually, this might actually be a difficult task...imagine you have some helpers or something). Let's say it's gone 10 meters, as marked on the road. Then it's speed is just 10 meters / 1 second=10 meters per second. Right?
Almost. What you've measured is the car's average speed over one whole second. But remember we want to find the speed of the car the instant it passes by your feet. Let's say it passed you by quite slowly but then managed to speed up incredibly quickly and travel 100 m by the time your stopwatch reached the one second mark. You wouldn't conclude that it was going 100 meters per second when it passed you.
So, you say, okay, let's not measure the distance it travels in a whole second after it passes me, as it can speed up, slow down, and do all sorts of crazy things in that time! Let's measure the distance it goes in just a tenth of a second!
This approach will have the same problem, but it's definitely getting us closer to what we want. The car can speed up or slow down in a tenth of a second just as it can speed up or slow down in a whole second, but it can't speed up as much! What you'll end up measuring though, is the average speed of the car over one tenth of a second. That's probably closer to the speed we're looking for.
Okay, so make it a hundredth of a second, or a thousandth! Well, you're getting the idea. No matter how small you make the time interval over which you're measuring, the car will always move some finite distance over that time interval. You can basically think of the speed as the distance you travel in some tiny time interval, divided by the time interval. If the car goes 10 millionths of a meter in 1 millionth of a second, then it's speed is very well approximated by .000001 meters/.0000001 seconds=10 meters per second.
[Now, if you want to be more precise, the above definition of speed doesn't quite cut it (but it's close enough, so you can probably skip this paragraph). Really, you take all these different tiny time intervals, say a thousandth, a millionth, a billionth, and a trillionth of a second, and mark off where the car is after each time interval. You find the average speed associated with each time interval as we did above for one second and one tenth of a second. If they're the same, great! You're done. That's your speed. But even if they're different, you'll notice that as you make the time interval smaller and smaller and smaller, the speed you calculate will get closer and closer to some value. That's the speed.]
Congratulations, you now more or less understand the idea behind the derivative—one of calculus's two essential ideas! In this case, what we were looking for was the speed. But here's how we found it: we took the change in position (how far the car moves) and divided by the time interval, meanwhile shrinking the time interval so that it was arbitrarily small. In math jargon, this looks like
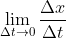
where x stands for position, t stands for time, and the Greek letter delta means "change in." This, then, we re-define as the derivative of position with respect to time. We solved our problem, and we generalized our solution to a definition, which will be very useful later on!
In the next post, I'll discuss the standard approach to calculus a little more thoroughly.

Calculus was developed as a solution to a very specific problem: the motion of objects through space. Though its applications range far beyond that problem, that original problem remains by far the best way to approach calculus since everybody already has intuition and experience with moving objects.
In a better world, then, calculus will always be approached from a physical perspective, since everyone already (sort of, at least) understands how things move around. Here's how. [This is, incidentally, what I did in the first day of AP physics class, but as you'll see, it's not terribly complicated, and (hopefully) most anyone can follow it.]
Imagine you're standing around with a stopwatch on a road that conveniently has length measurements posted all along it, and a car drives past you. Your task is to measure how fast the car is going the instant it passes the mark that's right at your feet. How do you do it?
Well, speed is just a measure of how far the car goes in some unit of time, say, a second, so you can just start your watch as the front wheels pass the mark by your feet, and then mark off where the front wheels of the car are when the watch reads exactly one second. (We can ignore the fact that, perceptually, this might actually be a difficult task...imagine you have some helpers or something). Let's say it's gone 10 meters, as marked on the road. Then it's speed is just 10 meters / 1 second=10 meters per second. Right?
Almost. What you've measured is the car's average speed over one whole second. But remember we want to find the speed of the car the instant it passes by your feet. Let's say it passed you by quite slowly but then managed to speed up incredibly quickly and travel 100 m by the time your stopwatch reached the one second mark. You wouldn't conclude that it was going 100 meters per second when it passed you.
So, you say, okay, let's not measure the distance it travels in a whole second after it passes me, as it can speed up, slow down, and do all sorts of crazy things in that time! Let's measure the distance it goes in just a tenth of a second!
This approach will have the same problem, but it's definitely getting us closer to what we want. The car can speed up or slow down in a tenth of a second just as it can speed up or slow down in a whole second, but it can't speed up as much! What you'll end up measuring though, is the average speed of the car over one tenth of a second. That's probably closer to the speed we're looking for.
Okay, so make it a hundredth of a second, or a thousandth! Well, you're getting the idea. No matter how small you make the time interval over which you're measuring, the car will always move some finite distance over that time interval. You can basically think of the speed as the distance you travel in some tiny time interval, divided by the time interval. If the car goes 10 millionths of a meter in 1 millionth of a second, then it's speed is very well approximated by .000001 meters/.0000001 seconds=10 meters per second.
[Now, if you want to be more precise, the above definition of speed doesn't quite cut it (but it's close enough, so you can probably skip this paragraph). Really, you take all these different tiny time intervals, say a thousandth, a millionth, a billionth, and a trillionth of a second, and mark off where the car is after each time interval. You find the average speed associated with each time interval as we did above for one second and one tenth of a second. If they're the same, great! You're done. That's your speed. But even if they're different, you'll notice that as you make the time interval smaller and smaller and smaller, the speed you calculate will get closer and closer to some value. That's the speed.]
Congratulations, you now more or less understand the idea behind the derivative—one of calculus's two essential ideas! In this case, what we were looking for was the speed. But here's how we found it: we took the change in position (how far the car moves) and divided by the time interval, meanwhile shrinking the time interval so that it was arbitrarily small. In math jargon, this looks like
where x stands for position, t stands for time, and the Greek letter delta means "change in." This, then, we re-define as the derivative of position with respect to time. We solved our problem, and we generalized our solution to a definition, which will be very useful later on!
In the next post, I'll discuss the standard approach to calculus a little more thoroughly.

Subscribe to:
Posts (Atom)